Experimental methods of determination of mechanical characteristics of micro and nanoobjects

In recent years, in view of the evolution of nanotechnology, the study of mechanical properties of nano-dimensional objects has become important. At the same time, many investigators pointed to a discrepancy between values of mechanical characteristics of nano-objects obtained in experiments and ones known in continual theory. One of the reasons consists in the following. At experiments with nano-objects the measuring equipment, being micro-objects, essentially influences on the researched object. This fact as a rule is ignored, that leads to inexact or even incorrect interpretation of experimental data. The purpose of the investigation consists in development of the theoretical foundation of experimental approaches to determination of stiffness parameters of nano-objects. One of the most efficient methods for the determination of elastic moduli used in macro-mechanics is based on the measurement of the eigenfrequencies of objects under study. The nuances of applying of this method for nano-objects are discussed below.

Method of determination of mechanical parameters of nano-objects, oriented on optical methods of measurement of eigenfrequencies

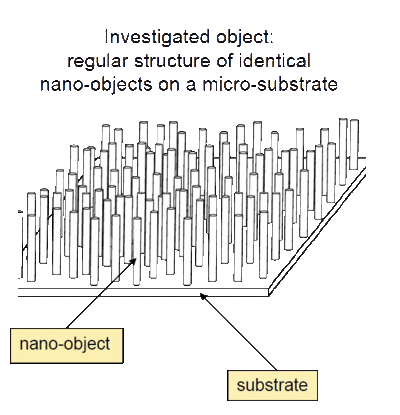
The measurement of nanoobject frequencies, in particular, on the basis of optical methods turns out to be problematic. Mechanical aspects of these methods consist in the following. The object under study is fixed on a frame of the macroscopical sizes and exited by a laser ray. Then amplitudes of oscillating of some point of object are measured with the help of the second laser ray. The signal is transformed in electric one. The received spectrogram is analyzed with the help of a spectrometer and as a result eigenfrequencies of object are determined. The main, thought not exclusive, limitation upon the application of optical methods is the fact that the laser-ray cross section is not a point but a spot whose diameter is on the order of the light wavelength. If the size of an object under investigation is smaller than the diameter of the laser ray, the measurement results are meaningless. Thus, measurement of eigenfrequencies of one nanoobject by using the optical methods is not possible. Meanwhile, the use of optical methods makes it possible to measure eigenfrequencies for systems containing microscopic-size substrate (micro-substrate) and a regular structure of identical nanoobjects. As a result, two problems arise that lie at the interface between mechanics and experimental physics.

• The first problem consists in the determination of the elastic moduli of nanoobjects under conditions in which the frequencies of a combined system of a micro-substrate and nanoobjects and elastic properties of isolated-microsubstrate are known.
• The second problem is associated with the possibility of extracting the nanoobject eigenfrequencies from a spectrum of microsubstrate - nanoobjects system.

We suggest a method for the determination of the eigenfrequencies of certain nanostructures (e.g., nanotubes and nanocrystals). The method is based on measuring eigenfrequencies of a system consisting of a highly oriented array (lattice) of identical nanotubes or nanocrystals located on a substrate. As a rule, the sizes of these nanoobjects in the array are approximately the same, which makes it possible to use the microscopic size of this array to study nanoobject properties by the determination of first eigenfrequencies for either nanotube - lattice or nanocrystal - substrate system. We show that, using the found spectrum of the lattice - substrate system and the substrate spectrum, it is possible to determine eigenfrequencies of the unique nanoobject. This allows us to determine nanoobject eigenfrequencies on the basis of data obtained for the microobject. The method is especially effective in a case when first eigenfrequencies of nanoobjects are comparable to first eigenfrequencies of a substrate. The main restriction of the method is the frequency range of measuring devices. If eigenfrequencies of nonoobjects are too high, to measure them will not be possible.

List of publications

1. Eremeyev V.A., Ivanova E.A., Morozov N.F., Solov'ev A.N. On the determination of eigenfrequencies for nanometer-size objects. // Doklady Physics. 2006. Vol. 51, N 2. P. 93-97.
2. Eremeyev V.A., Ivanova E.A., Morozov N.F., Solov'ev A.N. Method of determining of eigenfrequencies of an ordered system of nanoobjects. // Technical Physics. 2007. V. 52, No 1. P. 1-6.
3. Eremeyev V.A., Ivanova E.A., Morozov N.F., Strochkov S.E. Natural Vibrations of Nanotubes. // Doklady Physics. 2007, Vol. 52, N. 8. P. 431-435.
4. Eremeyev V.A., Ivanova E.A., Morozov N.F., Strochkov S.E. The Spectrum of Natural Oscillations of an Array of Micro- or Nanospheres on an Elastic Substrate. // Doklady Physics. 2007. Vol. 52, N 12. P. 699-702.
5. Eremeyev V.A., Ivanova E.A., Morozov N.F. Mechanical Problems in Nanotechnology. // Proceedings of the Saratov University. 2008. Vol. 8. Ser. Mathematics. Mechanics. Informatics. Issue 3. P. 25-32. (In Russian)
6. Eremeyev V.A., Ivanova E.A., Morozov N.F., Strochkov S.E. Natural vibrations in a system of nanotubes. // Journal of Applied Mechanics and Technical Physics. 2008. Vol. 49. N 2. P. 291-300.
7. Eremeyev V.A., Ivanova E.A., Indeitsev D.A. Wave processes in nanostructures formed by nanotube arrays or nanosize crystals. // Journal of Applied Mechanics and Technical Physics. 2010. Vol. 51. N 4. P. 569-578.
8. Eremeyev V.A., Ivanova E.A., Morozov N.F. Some problems of nanomechanics. // Fizicheskaya Mezomekhanika. 2013. Vol. 16. N 4. P. 67-73. (In Russian)

Method of determination of mechanical parameters of nano-objects, oriented on usage of an atomic force microscope

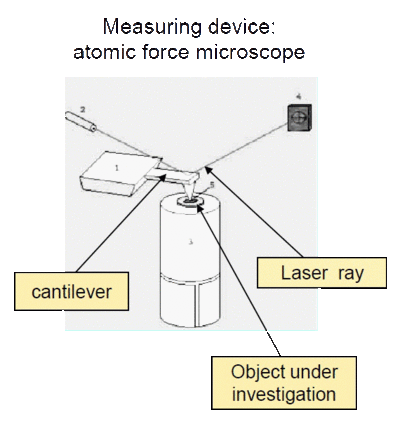
Now investigation of properties of nanoobjects, including measurement of their eigenfrequencies, is carried out by using sound microscopy. In particular, for these purposes atomic force microscope (AFM) is used. The method of measurement of eigenfrequencies, based on use of AFM, has the restrictions and lacks which are caused by distinction meanwhile, that in principle it is possible to measure by this method, and that it is possible to measure really on the modern equipment. We list the problems arising at realization of this method:

1. The frequency range accessible to measurement is limited. Its expansion aside the maximal frequency needs decrease of weight (sizes) of cantilever and (or) increase in its stiffness.
2. Fixing of a nanoobject should be carried out so that a substrate on which it is located, would not influence eigenfrequencies of the nanoobject, otherwise there will be the additional difficulties connected to interpretation of results of measurements and determination of properties of the nanoobject.
3. The needle of a cantilever is in contact to researched object and influences it. As a result, we are measuring not eigenfrequencies of the nanoobject but eigenfrequencies of a system containing nanoobject and cantilever.

Two problems arise that lie at the interface between mechanics and experimental physics.

• The first problem consists in the determination of the elastic moduli of nanoobjects by using the frequencies of a combined system of nanoobject and cantilever.
• The second problem is a development of conditions of experiment, such that it will be possible to extract eigenfrequencies of a nanoobject from a spectrum of a combined system of nanoobject and cantilever.

We suggest a method for the experimental determination of stiffness parameters which is based on an effect of dynamic damping of oscillations. The method gives possibility to extract eigenfrequencies of a nanoobject under study from the spectrum of the system.

List of publications

1. Ivanova E.A., Indeitsev D.A., Morozov N.F. On the determination of the rigidity parameters of nanoobjects. // Technical Physics. 2006. V. 51, issue 10. P. 1327-1333.
2. Ivanova E.A., Indeitsev D.A., Morozov N.F. On the determination of rigidity parameters for nanoobjects. // Doklady Physics. 2006. Vol. 51, N 10. P. 569-573.

Method of experimental determination of bending stiffness of nano-shells

Experimental determination of the bending stiffness of nanosize shells presents a serious problem, because for such widespread nanoobjects as nanotubes and fullerenes under arbitrary deformation, the material is subjected to both bending and tension. Therefore, all parameters (e.g., eigenfrequencies) that can be measured directly are complicated functions of both bending and tension stiffness. In recent years, together with nanotubes and fullerenes, nanoobjects of a more intricate configuration have been obtained. Nanosize cylindrical helices are of particular interest in connection with the possible experimental determination of bending stiffness. This is due to the fact that 1) in helical shells under arbitrary deformation, the material is mainly bent, so that material tension effect can be neglected when interpreting experimental data; and 2) eigenforms of oscillating of helical shell include not only rather specific eigenforms, but also "rod" ones (i.e. such eigenforms that the configuration of an axis represents the eigenform of oscillating of a rod). The latter statement is illustrated by figure, which presents the first four helical shell oscillating eigenforms. The "rod" oscillations of helical shells are much more easily observed, than cylindrical shell oscillations associated with pure bending of the material.

It is necessary to note one more important fact. The main obstacle for an experimental research of dynamics of nanoobjects is that their eigenfrequencies, as a rule, lay above a frequency range of measuring devices. This problem can be solved if a helical shell is used as the object of research. Eigenfrequencies of helical shell, as well as eigenfrequencies of a rod, are inversely proportional to a length squared. Therefore, increasing length of a helical shell it is possible to achieve decrease in frequencies to the values accessible to the modern measuring equipment. At the same time, it is well-known, that bending stiffness of a shell depends only on properties of a material and thickness, and does not depend on other sizes of a shell and its configuration. Therefore values of bending stiffness, obtained as a result of experiments with helical shells, it is possible to use for other types of nano-shells, made of the same material and having the same thickness. Thus, carried out analysis of helical shell dynamics may be a theoretical foundation for experimental determination of the bending stiffness of nanoshells.

List of publications

1. Ivanova E.A., Morozov N.F. An approach to the experimental determination of the bending stiffness of nanosize shells. // Doklady Physics. 2005. Vol. 50, N 2. P. 83-87.
2. Ivanova E.A., Morozov N.F., Semenov B.N., Firsova A.D. On determination of elastic modula of nanostructures: theory calculations and experimental method. // Izvestiya RAN. Mekhanika Tverdogo Tela. 2005. N 4. P. 75-85. (In Russian)
3. Ivanova E.A., Morozov N.F. On the determination of the flexural rigidity of nanoshells. // Journal of Mathematical Sciences. 2009. Vol. 162. N 2. P. 205-210.

E.A. Ivanova Homepage