Driven oscillations of a mass on a nonlinear spring

Driven oscillations of a mass on a nonlinear spring

Annotation to the project

This project gives an idea about nonlinear oscillation of a mass with the periodic force acting on it.

Formulation of the problem

Let’s put that a mass on nonlinear spring has mass m and experiencing the action of an external force F, which has a law F = sin (t).

• Task: formulate the problem on JavaScript which modulate motion of a mass with different parameters of the system.
  

Overview

If the periodically changing of the external force is acting on the system, the system performs oscillations which repeat the pattern of changes of this force. Such oscillations are called forced.

F0 is the force amplitude and the greatest value of the force.

Because of the work of an external force, the maximum value of the potential energy of the spring and the kinetic energy of a mass increase. This will increase the loss on overcome the resistance forces. In the end the work of the external force will exactly offset the energy losses in the system. Further growth of the oscillations in the system will stop and oscillations will be established with a constant amplitude.

A typical plot of the amplitude function

Equation of motion: [math]m\ddot x = -kx -{k_1}x^3 + {F_0}sin(t) - B \dot x[/math]

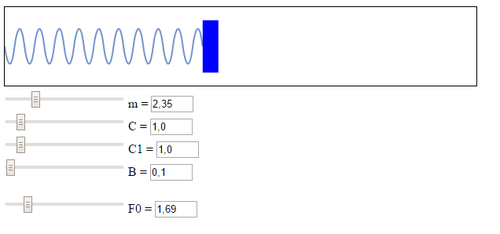
Visualization on JavaScript

Download program: SpringNoLine.rar

The Text of the program is written in JavaScript (developed by Pavel Kiselev):

  window.addEventListener("load", Main_Spring, true);
   function Main_Spring() {
   var canvas = spring_canvas;
   canvas.onselectstart = function () {return false;};     // prohibition of selection canvas
   var ctx = canvas.getContext("2d");                      // drawing at the ctx
   var w = canvas.width;                                   // the width of the window in the calculated coordinates
   var h = canvas.height;                                  // the height of the window in the calculated coordinates
   var Pi = 3.1415926;                                     // Pi
   var m0 = 1;                                             // weight scale
   var T0 = 1;                                             // time scale (the period of oscillation of the original system)
   var t = 0;
   var k0 = 2 * Pi / T0;                                   // frequency scale
   var C0 = m0 * k0 * k0;                                  // hardness scale
   var B0 = 2 * m0 * k0;                                   // viscosity scale
   var omega = 10;
   
   // *** Creating the physical parameters ***
   var F = 80;
   var m = 1 * m0;                                         // weight
   var C = 1 * C0;                                         // rigidity
   var C1 = 1 * C0;                                        // rigidity1
   var B = .1 * B0;                                        // viscosity
   
   slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1);
   slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1);
   slider_C1.value = (C / C0).toFixed(1); number_C1.value = (C / C0).toFixed(1);
   slider_B.value = (B / B0).toFixed(1); number_B.value = (B / B0).toFixed(1);
   slider_F.value = (F / 40).toFixed(1); number_F.value = (F / 40).toFixed(1);

   // *** Creating the computing parameters ***

   var fps = 300;                                  // frames per second 
   var spf = 100;                                  // steps per frame   
   var dt  = 0.05 * T0 / fps;                      // integration step (calculation quality)  
   var steps = 0;                                  // the number of integration steps

   function setM(new_m) {m = new_m * m0;}
   function setC(new_C) {C = new_C * C0;}
   function setC1(new_C1) {C1 = new_C1 * C0 * 0.067;}
   function setB(new_B) {B = new_B * B0;}
   function setF(new_F) {F = new_F * 40;}

   slider_m.oninput = function() {number_m.value = slider_m.value;       setM(slider_m.value);};
   number_m.oninput = function() {slider_m.value = number_m.value;       setM(number_m.value);};
   slider_C.oninput = function() {number_C.value = slider_C.value;       setC(slider_C.value);};
   number_C.oninput = function() {slider_C.value = number_C.value;       setC(number_C.value);};
   slider_C1.oninput = function() {number_C1.value = slider_C1.value;       setC1(slider_C1.value);};
   number_C1.oninput = function() {slider_C1.value = number_C1.value;       setC1(number_C1.value);};
   slider_B.oninput = function() {number_B.value = slider_B.value;       setB(slider_B.value);};
   number_B.oninput = function() {slider_B.value = number_B.value;       setB(number_B.value);};
   slider_F.oninput = function() {number_F.value = slider_F.value;       setF(slider_F.value);};
   number_F.oninput = function() {slider_F.value = number_F.value;       setF(number_F.value);};

   var count = true;                   // system analysis
   var v = 0;                          // speed of a mass

   var rw = canvas.width / 30;         
   var rh = canvas.height / 1.5;
   var x0 = 15 * rw - rw / 2;          
   var y0 = rh / 1.33 - rh / 2;

   // spring settings
   var coil = 10;        // number of turns
   var startX = 0;       // spring fastening

   //  create a rectangle (mass)
   var rect = {
       x: x0,  width: rw,
       y: y0,  height: rh,
       fill: "rgba(0, 0, 255, 1)"      // colour
   };

   // capture a rectangle with the mouse
   var mx_;                                    // buffer position of the mouse (to calculate the speed of the ball when released)
   document.onmousedown = function(e) {        // function by pressing the mouse button
       var m = mouseCoords(e);                 // we get estimated coordinates of the mouse cursor

       var x = rect.x;
       var xw = rect.x + rect.width;
       var y = rect.y;
       var yh = rect.y + rect.height;
       if (x <= m.x && xw >= m.x   && y <= m.y && yh >= m.y) {
           if (e.which == 1) {                         // left mouse button is pressed
               rect.xPlus = rect.x - m.x;              // cursor shift relative to the cargo on the x
               rect.yPlus = rect.y - m.y;              // cursor shift relative to the cargo on the y
               mx_ = m.x;
               count = false;
               document.onmousemove = mouseMove;       // while a key is pressed, fanction of motions is correct
           }
       }
   };

   document.onmouseup = function(e) {            // function when you release the mouse button
   document.onmousemove = null;                  // when the key is released, no movement function
       count = true;
   };

   function mouseMove(e) {                     // function when you move the mouse, it works only while holding LKM
       var m = mouseCoords(e);                 // we get estimated coordinates of the mouse cursor
       rect.x = m.x + rect.xPlus;

// v = 6.0 * (m.x - mx_) / dt / fps; // inertia preservation

       v = 0;
       mx_ = m.x;
   }

   function mouseCoords(e) {                   // function returns the calculated coordinates of the mouse cursor
       var m = [];
       var rect = canvas.getBoundingClientRect();
       m.x = (e.clientX - rect.left);
       m.y = (e.clientY - rect.top);
       return m;
   }

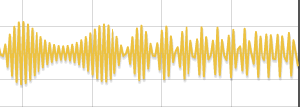
   //  plot
   var vGraph = new TM_graph(                  // determine the plot
       "#vGraph",                              // on html-element #vGraph
       250,                                    // the number of steps by "x" axis
       -1, 1, 0.2);                            //  min value of Y-axis, max value of Y-axis, Y-axis step

   function control() {
       calculate();
       draw();
       requestAnimationFrame(control);
   }
   control()

// setInterval(control, 1000 / fps); // start of the system

   function calculate() {
       if (!count) return;
       for (var s=1; s<=spf; s++) {
           var f = -B*v - C * (rect.x - x0) - C1*Math.pow(rect.x - x0,3)+2*F*Math.sin(t);
                       v += f / m * dt;
                       //console.log(f);
           rect.x += v * dt;
                       t+= dt;
           steps++;
           if (steps % 80 == 0) vGraph.graphIter(steps, (rect.x-x0)/canvas.width*2);   // infeed graph data
       }

   }

   function draw() {
       ctx.clearRect(0, 0, w, h);
               draw_spring(startX, rect.x, h/2, 10, 50);
       ctx.fillStyle = "#0000ff";
       ctx.fillRect(rect.x, rect.y, rect.width, rect.height);
   }

       function draw_spring(x_start, x_end, y, n, h) {
           ctx.lineWidth = 2;
       ctx.strokeStyle = "#7394cb";
               var L = x_end - x_start;
               for (var i = 0; i < n; i++) {
                       var x_st = x_start + L / n * i;
                       var x_end = x_start + L / n * (i + 1);
                       var l = x_end - x_st;
                       ctx.beginPath();
                       ctx.bezierCurveTo(x_st, y, x_st + l / 4, y + h, x_st + l / 2, y);
                       ctx.bezierCurveTo(x_st + l / 2, y, x_st + 3 * l / 4, y - h, x_st + l, y);
                       ctx.stroke();
               }
       }

}